MD5 message digest algorithm:
The MD5 message-digest algorithm was developed by Ron Rivest at MIT. Until the last few years, when both brute-force and cryptanalytic concerns have arisen, MD5 was the most widely used secure hash algorithm.
MD5 logic. The algorithm takes as input a message of arbitrary length and produces as output a 128-bit message digest. The input is processed in 512-bit blocks.
The processing consists of the following steps:
Step 1: Appending padding bits. The massage is padded so that its length in bits is congruent to 448 modulo 512 (length ≡ 448 mod 512). That is, the length of the padded message is 64 bits less than an integer multiple of 512 bits. Padding is always is added, even if the message is already of the desired length. For example, if the message is 448 bits long, it is padded by 512 bits to a length of 960 bits. Thus, the number of padding bits isin the range of 1 to 512. The padding consists of a single 1-bit followed by the necessary number of 0-bits.
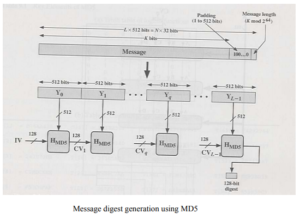
Step 2: Append length. A 64-bit representation of the length in bits of the original message (before the padding) is appended to the result of step 1 (least significant byte first). If the original length is greater than 264, then only the low-order 64 bits of the length are used. Thus, field contains the length of the original message, modulo 264. The outcome of the first two steps yields a message that is an integer multiple of 512 bits in length.For example, if the , Message is represented as the sequence of 512-bit blocks YY Y 01 1 L ,, , … − , so that the total length of the expanded message is L × 512 bits. Equivalently, the result is a multiple of 16 32-bit words. Let M[ ] 0 1 …N − denote the words of the resulting message, with N an integer multiple of 16. Thus, N = L ×16.
Step 3: Initialize MD buffer. A 128-bit buffer is used to hold intermediate and final results of the hash function.The buffer can be represented as four 32-bit registers (A, B, C, D). These registers are initialized to thefollowing 32-bit integers (hexadecimal values):
A = 67452301
B = EFCDAB89
C = 98BADCFE
D = 10325476
These values are stored in little-endian format, which is the least significant byte of a word in the low-address byte position. As 32-bit strings, the initialization values (in hexadecimal) appears as follows:
Word A: 01 23 45 67
Word B: 89 AB CD EF
Word C: FE DC BA 98
Word D: 76 54 32 10
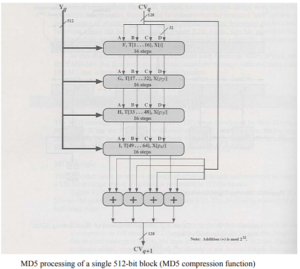
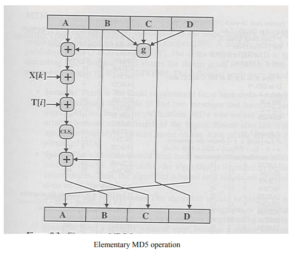
Step 4: Process message in 512-bit (16-word) blocks. The heart of the algorithm is a compression algorithm that consists of four “rounds” of processing; this module is labeled HMD5. The four rounds have the similar structure,but each uses a different primitive logical function, referred to as F, G, H, and I in the specification. Each round takes as input the current 512-bit block being processed (Yq) and the 28-bit buffer value ABCD and updates the contents of the buffer. Each round also makes use of one-fourth of a 64-element table T[ ] 1 64 … , constructed from the sine function. The ith element of T, denoted T[i], has the value equal to the integer part of 232 × abs i (sin( )) , where I is in radians.
Step 5: Output. After all L 512-bit blocks have been processed, the output from the Lth stage is the 160-bit message digest.